[2021 SCPC 2차 예선]

직8각형

평면상에서 한 변의 길이가 K (K는 자연수)인 정사각형 5개가 <그림 1>에서 보인 것처럼 ✚모양으로 배치되어 있을 때, 외곽에 놓인 8개의 점이 만드는 8각형을 길이가 K인 ‘직8각형’이라 부른다.

그리고 외곽에 놓인 8개의 점을 직8각형의 꼭지점이라 부른다.

직8각형 꼭지점의 xy 좌표는 모두 정수이다.

길이가 K인 직8각형을 구성하는 8개의 꼭지점을 시계방향 순서로 \(p_0,…,p_7\)이라 둘 때, \(p_0\)의 좌표가 \((x_0,y_0)\) 라면 \(p_1\)의 좌표는 \((x_0,y_0+K)\)이고, \(p_2\)의 좌표는\((x_0+K,y_0+2K)\)이며, 유사하게 나머지 점들의 좌표도 결정된다. 





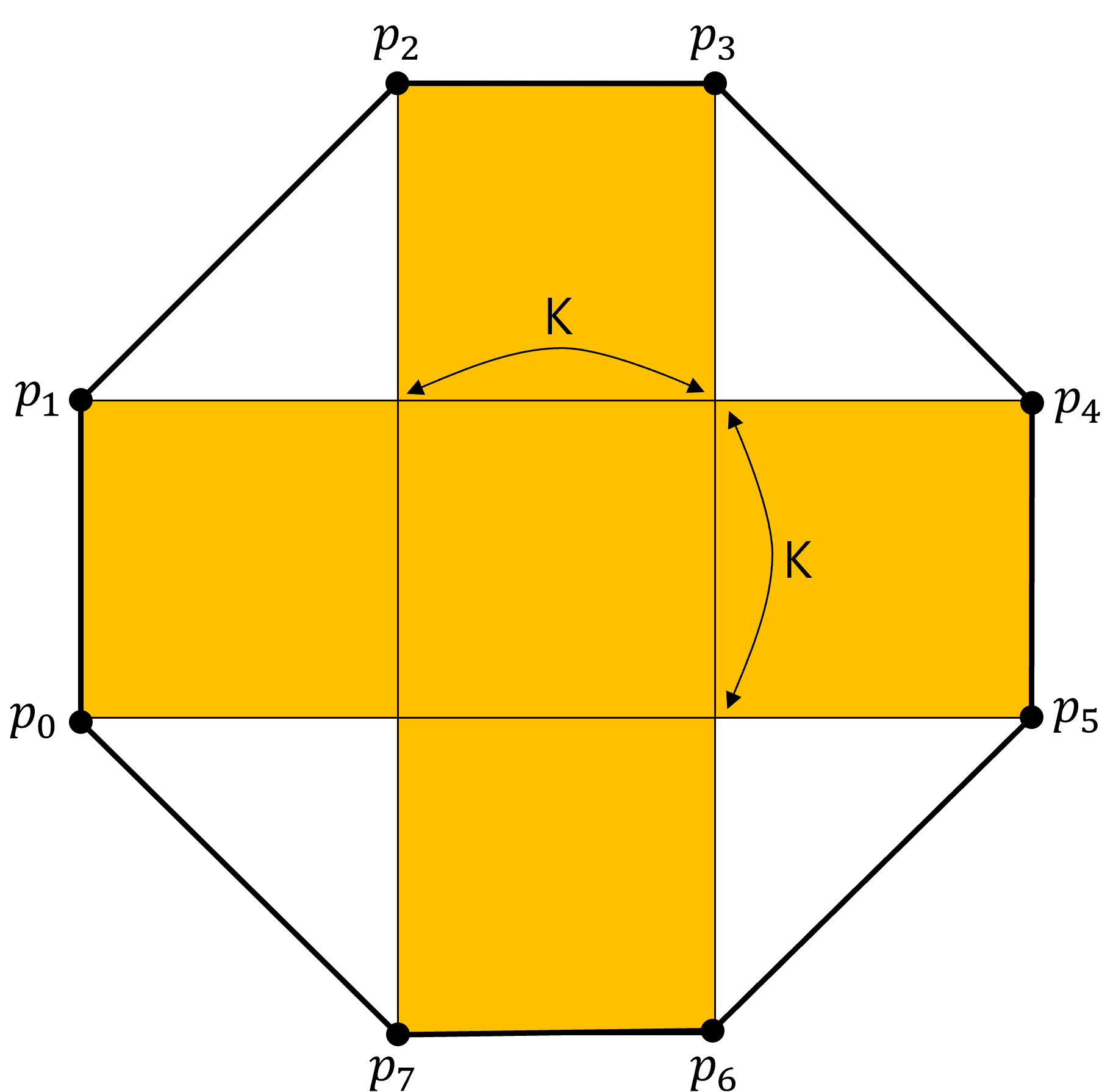
<그림 1>





임의의 위치에 놓여 있는 8개의 각 점을 이동하여 길이가 K인 직8각형을 만들고자 한다.

좌표 \((x_s,y_s)\)에 놓인 한 점을 좌표 \((x_t,y_t)\)로 이동할 때,

이동거리는 \( |x_s-x_t |+|y_s- y_t |\)이다. 여기서 \(|a|\)는 \(a\)의 절대값을 의미한다.



<그림 2>에선 임의의 위치에 놓여 있는 8개의 점(검은 색)을 이동하여 길이가 3인 직8각형을 만든 예이다.

직8각형 꼭지점 \(p_0,…,p_7\) 각각에 대해 이동거리는 각각 2,3,6,2,2,1,3,3이고 이동거리의 합은 22이다. 





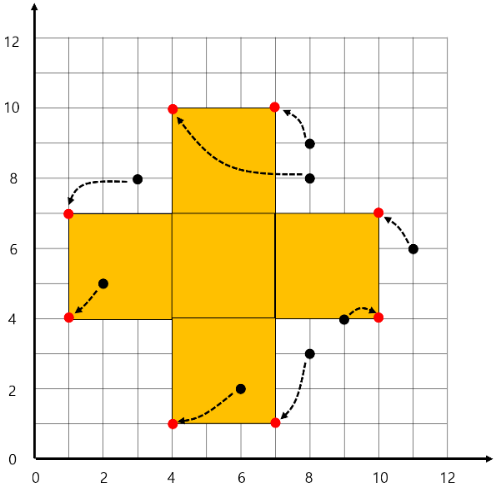
<그림 2>





한편, <그림 3>은 <그림 2>에서 보인 점들과 동일한 위치에 놓인 검은 점들을 이동하여 길이가 2인 직8각형을 만든 예를 보여 준다.

이처럼 만들어진 직8각형 꼭지점 \(p_0,…,p_7\) 각각에 대해 이동거리는 각각 1,1,3,2,3,1,1,2이고 이동거리의 합은 14가 된다.





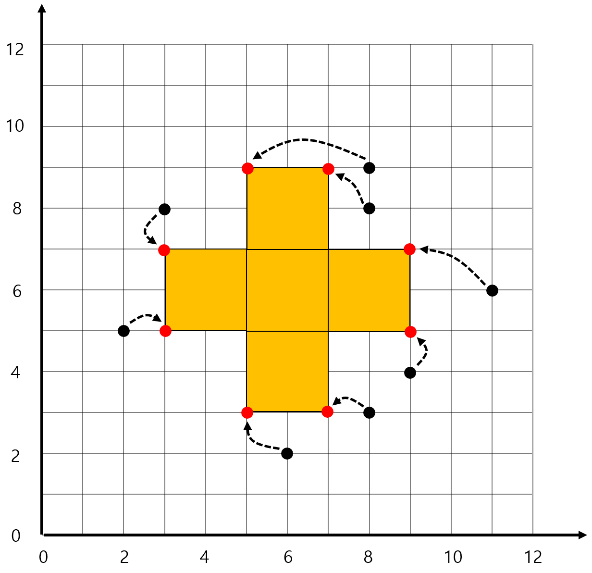
<그림 3>





평면 상에 놓인 8개의 점에 관한 좌표와 정수 K가 주어질 때, 이들을 이동하여 길이가  K인 직8각형을 만들기 위해 필요한 점들의 이동거리 합의 최소값을 출력하는 프로그램을 작성하시오.


그림 1

입력

입력 파일에는 여러 테스트 케이스가 포함될 수 있다.

파일의 첫째 줄에 테스트 케이스의 개수를 나타내는 자연수 T 가 주어지고, 이후 차례로  T 개의 테스트 케이스가 주어진다. \((1 ≤ T ≤ 200) \)



각 테스트 케이스의 첫 줄에는 정수 \(K(1≤K≤10^8)\) 가 주어진다.

이어지는 8개의 각 줄에는 점의 좌표\( x_i,y_i\ (1≤i≤8,\ -10^8≤x_i,y_i≤10^8)\)가 공백으로 구분되어 주어진다.

모든 점의 좌표는 정수이며, 평면 상에서 서로 다른 점이다.


출력

각 테스트 케이스의 답을 순서대로 표준출력으로 출력하여야 하며, 각 테스트 케이스마다 첫 줄에는 “Case #C”를 출력하여야 한다. 이때 C는 테스트 케이스의 번호이다.

그 다음 줄에, 주어진 정수 K와 평면 상에 놓인 8개의 점에 관한 좌표에 대해, 이 점들을 이동하여 길이가  K인 직8각형을 만들기 위해 필요한 점들의 이동거리 합의 최소값을 출력하시오.

입출력예

입력
2
2
2 5
8 9
8 5
3 8
6 2
8 8
9 4
11 6
3
2 5
3 8
6 2
8 8
8 9
8 5
9 4
11 6
출력
Case #1
14
Case #2
18

돌아가기

댓글